Formulario di geotecnica

FORMULARIO DI GEOTECNICA

• INDICE

---

#

FASI DEL TERRENO

IL SISTEMA TERRENO (Sistema ideale)

 

TE = S + W + G (SISTEMA MULTIFASE*)

TE (terreno)  – S (fase solida)-  W (fase liquida) – G (fase gassosa)

*in prima approssimazione è un sistema a tre fasi

#

PESI E VOLUMI

VOLUME

V_t = V_s + V_w + V_g     Volume totale         V_v = V_w + V_g    Volume dei vuoti

V_t (volume totale), V_s (volume parte solida), V_w (volume parte liquida), V_g (volume parte gassosa)

GRADO DI SATURAZIONE (G_S), INDICE DEI VUOTI (e) , POROSITA’ (n)

#

PESI

P_t = P_s + P_w  (peso totale)   con  Pg ≈ 0

Metodo di calcolo del w_n

Pw = Pcu  – Tar   (peso dell’acqua contenuto in un campione di terreno naturale)

Ps = Pcs – Tar     (peso del materiale solido essiccato in forno a 100°C)

Tar       (tara)
Pcu       (peso del campione umido + Tar)
Pcs       (peso del campione solido + Tar)

 

PESO SPECIFICO (γ)

RELAZIONI FONDAMENTALI

#

RELAZIONI FRA e ed n

#

RELAZIONI FRA γ, G_S, w_n, e ed n

Relazioni relative al γ_n

γ_n = (1- n) γ_s + (n G_S γ_w)                                 γ_n= (1-n) γ_s  + (n · γ_w)

Relazioni relative al γ_sat

Υ_sat = Υ’ + Υ_w

Relazioni relative al γ_d (γ_s)

Relazioni relative al γ’

Relazioni relative al Gs

Relazioni relative ad e ed n

CARATTERISTICHE DEL TERRENO RICAVATE CON PROVE SPERIMENTALI

Caratteristiche generali

Densità relativa (D_r)

Densità totale (ρ)

Caratteristiche e classificazione dei terreni mediante metodi sperimentali 

Costruzione della curva granulometrica

Materiali a grana fine  Ø < 74 μ  – AREOMETRIA

Materiali a grana grossa Ø > 74 μ  – SEPARAZIONE  MECCANICA

Analisi granulometriche

Coefficiente di uniformità (C_U)

Coefficiente di curvatura (C_c)

LIMITI DI CONSISTENZA  (o LIMITI DI ATTENBERG ) (LL, LP, LR)

LIMITE LIQUIDO LIQUIDO (LL)

Misura di LL con il cucchiaio di Casagrande

Viene misurato il contenuto d’acqua w_L in corrispondenza del quale un provino di terreno, posto nel cucchiaio di Casagrande di dimensioni normalizzate, suddiviso in due parti con un apposito utensile solcatore, e fatto rimbalzare da un h = 10 mm determina la chiusura del solco per una l = 13 mm. 

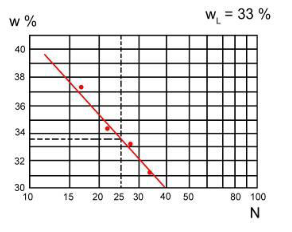
In almeno 4 ripetizioni va registrato il numero dei colpi (N_l) a cui si richiude il solco e misurato il contenuto d’acqua (w_l). Il limite LL (W_L %) è il valore corrispondente a 25 colpi ottenuto mediante interpolazione tra le misure eseguite (in scala semi logaritmica)

Misura di LL con il penetrometro

Il LL è fissato dal contenuto d’acqua w_L in corrispondenza del quale un provino di terreno, posto in un contenitore di dimensioni normalizzate, determina un dato affondamento di una punta conica appoggiata in verticale su di esso per 5 s. Ciò corrisponde ad una resistenza non drenata cu = 2 kPa

L’affondamento i di un cono con peso W è legato alla resistenza non drenata cu dalla:
Anche il metodo di Casagrande è una misura di resistenza, ma: in condizioni dinamiche e non statiche, ha un carattere spiccatamente empirico, si è dimostrato meno ripetibile e affidabile.
Le raccomandazioni europee (ETC5, EC7) suggeriscono l’adozione della punta conica
(quale che sia) per la misura del LL. Le misure sperimentali hanno dimostrato che w_L (Casagrande) > w_L (Fall cone).

 

LIMITE DI RITIRO (LR)

w_L peso dopo essiccamento senza perdita di volume del provino.

LIMITE PLASTICO (LP)

Contenuto d’acqua in corrispondenza del quale il terreno inizia a perdere il suo comportamento plastico.

• 15 g di terra, opportunamente  preparata con acqua distillata, viene lavorata con le mani su di un piano di vetro fino a formare, prima una pallina e poi un cilindretto di 3,2 mm di diametro.
• Nel campione si formeranno fessure in corrispondenza del LP
• Queste fessure frammenteranno il cilindretto in altri più corti. Se il cilindretto di terra si rompe prima che il diametro di 3,2 mm sia stato raggiunto, occorre bagnare ulteriormente la terra e ripetere l’operazione, se invece è possibile scendere sotto i 3,2 mm senza che il campione di terreno si rompa in frammenti di 5-10 mm di lunghezza occorre ripetere l’operazione finché il cilindretto essiccandosi per effetto delle manipolazioni, si divida in cilindretti di queste dimensioni (5-10 mm). A questo punto si misura il contenuto di acqua di alcuni cilindretti. La prova deve essere ripetuta almeno tre volte, le tre determinazioni non devono differire tra loro oltre una unità percentuale. Altrimenti la prova va ripetuta scartando i valori ottenuti in precedenza. Il risultato sarà dato dalla media delle tre determinazioni, deve essere arrotondato all’unità. Tale valore è per definizione pari al Limite Plastico (Wp o LP). In alcuni casi il LP non è determinabile poiché è impossibile modellare la terra in cilindretti del diametro stabilito e la terra viene indicata come Non Plastica (NP).

INDICE PLASTICO (IP)

IP = W_L – W_p

INDICE DI CONSISTENZA (IC)

 

 

INDICE DI LIQUIDITA’ (IL)

 

 

---

ANALISI DELLE PRESSIONI NEL TERRENO

PRESSIONI VERTICALI IN UN TERRENO OMOGENEO

Pressione verticale in assenza di acqua – CASO 1

(vedi esempi – TERRENO OMOGENEO CASO 1)

Pressione verticale in presenza di acqua in condizioni idrostatiche terreno omogeneo – Falda al di sotto del P.C. (CASO 2)

Pressione efficace (σ’_v) ovvero pressione verticale dovuta al terreno immerso alla profondità z_x

(vedi esempi – TERRENO OMOGENEO CASO 2)

Pressione verticale in presenza di acqua in condizioni idrostatiche terreno omogeneo – Falda sul P.C. (CASO 3)

               (vedi esempi – TERRENO OMOGENEO CASO 3)

 

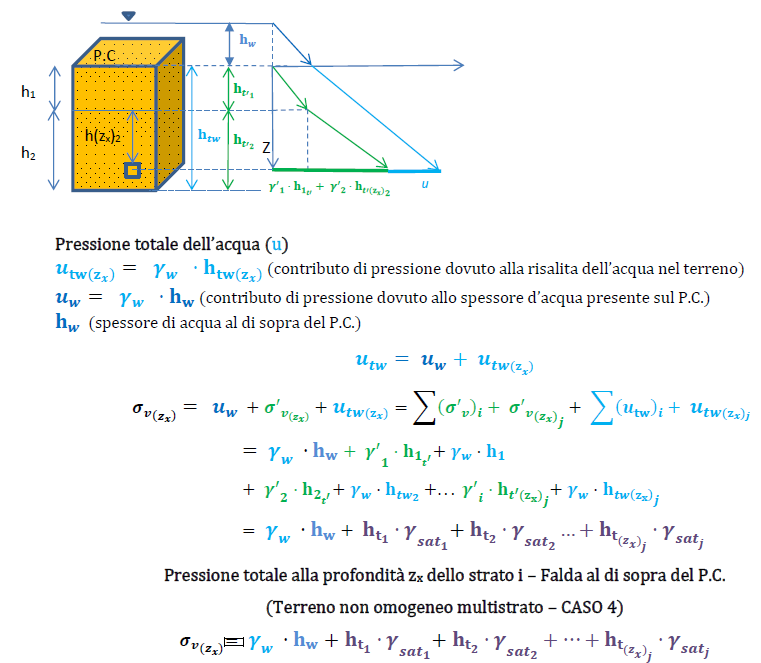
Pressione verticale in presenza di acqua in condizioni idrostatiche terreno omogeneo – Falda al di sopra del P.C. (CASO 4)

(vedi esempi – TERRENO OMOGENEO CASO 4)

Pressione totale su un terreno omogeneo in presenza o no di acqua in condizioni idrostatiche) (sintesi)

 

---

Calcolo dello spessore e della profondità in un terreno

z = (ξ – h _ξ)

z profondità dal P.C.
h _ξ  spessore esistente al di sopra della fondamentale e la quota considerata
 spessore totale
ξ (distanza totale dalla fondamentale al P.C.)

---

PRESSIONI VERTICALI IN UN TERRENO NON OMOGENEO MULTISTRATO (SENZA FILTRAZIONE)

ANALISI DEI CARICHI IN TERRENO MULTISTRATO IN CONDIZIONI IDROSTATICHE (SENZA FILTRAZIONE)

CASO 1 – Assenza di acqua (u  = 0)

vedi esempi

TERRENO NON OMOGENEO MULTISTRATO SENZA FILTRAZIONE – CASO 1

---

CASO 2 – Presenza di acqua – Livello di falda al di sotto del  PC. (u ≠ 0) (SENZA FILTRAZIONE)

(vedi esempi TERRENO NON OMOGENEO MULTISTRATO SENZA FILTRAZIONE – CASO 2)

---

CASO 3 – Presenza di acqua – Livello di falda coincidente con il P.C. (u ≠ 0)

Vedi esempi – TERRENO NON OMOGENEO MULTISTRATO SENZA FILTRAZIONE – CASO 3

---

TERRENO NON OMOGENEO MULTISTRATO SENZA FILTRAZIONE – CASO 3

 

vedi esempi

TERRENO NON OMOGENEO MULTISTRATO SENZA FILTRAZIONE – CASO 4

---

PRESSIONI VERTICALI IN UN TERRENO MULTISTRATO IN PRESENZA DI FILTRAZIONE

Teorema di Bernoulli

m_e = m_u   (nel caso di filtrazione all’interno del terreno in un sistema ideale chiuso la massa d’acqua in entrata deve essere uguale a quella in uscita)

e quindi

Q_e = Q_u (nel caso di filtrazione all’interno del terreno in un sistema ideale chiuso la portata d’acqua in entrata deve essere uguale a quella in uscita)

Altezze di carico

Coefficiente di permeabilità (k) e flusso dell’acqua attraverso un terreno

 

Valori tipici di k

k reale in terreno non omogeneo (multistrato)

---

PORTATA (Q)

CASI IN PRESENZA DI FILTRAZIONE (ΔH ≠ 0)

Filtrazione monodimensionale

Analisi del carico idraulico

Gradiente carico idraulico critico (i_c)

• in presenza di filtrazione ascendente

i_c = γ’/γ_w

Sifonamento 

• se i_c = i 

Verifiche SLU al sollevamento – UPL (D.M. 17.01.2018)

Condizione per la stabilità al sollevamento

V_inst,d ≤ G_stb,d + Rd

V_inst,d  (valore di progetto dell’azione instabilizzante)
dove V_inst,d = G_inst,d + Q_inst,d

Ginst,d  (pressioni idrauliche ottenuta considerando la parte permanente)
Qinst,d  (pressioni idrauliche ottenuta considerando la parte variabile)
G_stb,d    (valori di progetto delle azioni stabilizzanti)
Rd         (valori di progetto delle  resistenze)

Verifiche SLU idrauliche (UPL e HYD) 

 

Verifiche SLU al sifonamento – HYD (D.M. 17.01.2018)

Calcolo della pressione dell’acqua (u) in un sistema multistrato

Calcolo della pressione verticale (σ_v) totale in sistema multistrato in presenza di filtrazione

Calcolo della pressione dell’acqua (u) in un sistema multistrato

---

CASO 1 – Moto di filtrazione verso l’alto (segno positivo) – Livello di falda al di sotto del  PC. (ΔH > 0)

vedi esempi – TERRENO NON OMOGENEO MULTISTRATO CON FILTRAZIONE CASO 1

---

CASO 2 – Moto di filtrazione verso l’alto (segno positivo) – Livello di falda al di sotto del  PC. 

 vedi esempi – TERRENO NON OMOGENEO MULTISTRATO CON FILTRAZIONE

CASO 2

 

---

CASO 3 – Moto di filtrazione verso l’alto – Livello di falda al di sopra del PC(u ≠ 0)

 (vedi esempi TERRENO NON OMOGENEO MULTISTRATO CON FILTRAZIONE – CASO 3)

---

FILTRAZIONE BIDIMENSIONALE

Filtrazione in mezzo omogeneo isotropo (per cui k = cost) (sistema confinato)

Modello bidimensionale di filtrazione

condizione con c_n = 1, a_n  ≈  b_n (campo approssimato ad un quadrato)

---

Calcolo della portata (filtrazione in mezzo omogeneo isotropo (per cui k = cost e i=cost) (sistema confinato)

Come disegnare le linee di flusso

---

 

Portata di filtrazione (Q_f) in mezzo omogeneo isotropo (per cui k e i = cost) (sistema confinato)

---

Calcolo della pressione neutra (u) in un punto alla profondità z_x in caso di filtrazione bidimensionale (vedi costruzione grafica)

Calcolo della pressioni efficaci (filtrazione in mezzo omogeneo isotropo (per cui k = cost, i=cost) (sistema confinato)

Caso in cui sia a valle che a monte vi sia uno spessore di terreno sotto falda (VEDI ESEMPI)

Caso in cui sia a valle che a monte la falda si trova al di sopra del P.C. (VEDI ESEMPI)

---

FILTRAZIONE BIDIMENSIONALE

Filtrazione bidimensionale in mezzo non omogeneo anisotropo – (per cui  k_h < k_v k_h < k_v)(sistema confinato)

Costruzione della rete di flusso in mezzo anisotropo

• Disegnare una rete di flusso in un mezzo anisotropo
• Definire i parametri reali della geometria del problema come il fattore di deformazione (f_d )
• Utilizzare la deformazione geometrica necessaria per risolvere il problema utilizzando le regole di disegno della rete di flusso in mezzi isotropi;
• Apportare le correzioni al disegno per rappresentare il reale processo di filtrazione.

Filtrazione bidimensionale in mezzo non omogeneo isotropo – (per cui  k₁ ≠ k₂ ; k_v= k_h)

Modello di filtrazione attraverso terreni a differente permeabilità

 

---

Cedimento e consolidazione

Un carico agente su un terreno coesivo saturo d’acqua produce su di esso deformazioni cosi distinte:
• cedimento immediato (S_i), a cui corrispondono minime variazioni di volume;
• cedimento di consolidazione primaria (C_p) conseguente ad una variazione di volume (ΔV) e ad espulsione dell’acqua, ovvero diminuzione dell’indice dei vuoti (e) che è collegata alla porosità (n);
• cedimento di consolidazione secondaria (Cs) con variazione di volume

Possiamo quindi definire il cedimento totale come:

S_t = S_i + S_c

S_t = S_i + (S_p + S_s) = S_i + S_c

S_t  (cedimento totale)
S_i  (cedimento immediato)  al’inizio posseggono una piccolissima parte reversibile
S_c = S_p + S_s (cedimento di consolidazione)
S_p  (o anche S_e) (cedimento primario o di consolidazione)
S_s  (cedimento secondario)

Materiali lapidei (rocce)

S_t (cedimento totale) ≈ 0

Terreni incoerenti (sabbie, Ghiaie, Limi)

S_t = S_i

Terreni coerenti (argille)

S_t = S_i + (S_e + S_s) = S_i + S_c

Valori tipici

S_i = 0,1 S_e

S_s = 0 ⇒  S_c = S_e

S_t = 0,1 S_e + S_e = 1,1 S_e (cedimento totale)

Cedimento  immediato

Per fondazioni superficiali su terreni sabbiosi (sabbia, ghiaia fine). Vengono utilizzate le prove penetrometriche (SPT).

• per fondazioni superficiali flessibili (D=0, H = ∞)

S_i  (cedimento immediato medio della fondazione)
Δq (incremento di carico medio applicato sul piano di posa)
B (larghezza della fondazione)
v = 0,3 (rapporto di Poisson)
E (modulo di elasticità del terreno) [E = 766 Nspt per i terreni incoerenti e E = 375 Cu per terreni coerenti]
I_s (fattore di influenza dipendente dalla posizione del punto di calcolo), dalla forma della fondazione (L/B) e dalla rigidezza della fondazione

• per fondazioni superficiali rigide 

S_t (cedimento totale fondazione rigida) ≈ 0,8 (cedimento totale fondazione flessibile)

Cedimento immediato secondo Schmertmann

CZ  = 1 – 0,5 (σ’_vo / Δq )  (fattore di correzione della profondità)
σ’_vo (pressione effettiva verticale)

CC = 1 + 0,2 log (t / 0,1) (fattore di creep)
t (tempo dopo applicazione del carico)

Δq (incremento di carico medio applicato sul piano di posa della fondazione)

I_z (fattore d’influenza  – vedi grafico, dove B e è la larghezza della fondazione)

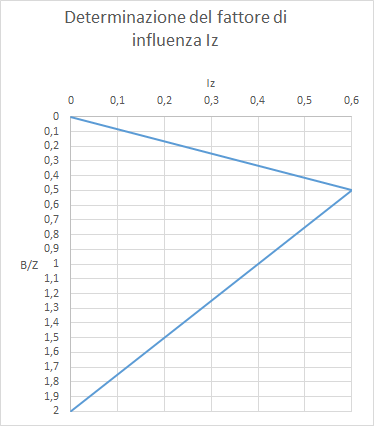
H spessore dello strato
E (modulo elastico)

 

Cedimento immediato secondo Schmertmann metodo semplificato

S_i = 0,7 Δq B (N₁)₆₀

(N₁)₆₀ (resistenza penetrometrica corretta)

Cedimento immediato e cedimento di consolidazione secondo Skempton-Bjorrum (argille sature)

S_t = S_i + S_c

 

Cedimento immediato secondo Skempton-Bjorrum

• cedimento immediato in condizioni non drenate

E_s (modulo elastico non drenato)
μ₀ μ₁ (coefficienti di influenza – vedi figura)

Δq (carico di esercizio)
B (lunghezza della fondazione)

Cedimento di consolidazione secondo Skempton-Bjorrum 

S_t = S_i + S_c  (cedimento totale)

S_c = μ S_ed  (cedimento di consolidazione)

S_t = S_i + μ S_ed

ARGILLE NC

S_i = 0,1 S_ed       S_c = S_ed         S_t = 1,1 S_ed

ARGILLE OC

S_i = 0,6 S_ed      S_c = 0,4 S_ed     S_t = S_ed

μ (coefficiente adimensionale funzione del parametro di sovrappressione neutra A di Skempton – vedi figura)

Determinazione del valore di μ

B (larghezza della fondazione)
H (spessore dello strato)

Cedimento immediato metodo di Anagnastropoulos

S_i = (6,02 Δq^0,36 B^0,7) /  N^1,2   [cm]

B (larghezza della fondazione)
N (media non corretta di Nspt ad una alla profonditò B sotto la fondazione)

 

Cedimento immediato metodo di Meyerhof

C_D (fattore di conversione)
B  (larghezza della fondazione)
D (profondità della fondazione)
N’ (valore medio corretto di N_SPT)

*** sezione in costruzione ***

---

Cedimento edometrico (S_e)

CONDIZIONI REALI
Fasi favorevoli/sfavorevoli al cedimento in un terreno coerente (argilla)
t0	t ≈  0	Δq = Δu	terreno saturo	cedimento impedito	Sc = 0
t1	t > 0	Δq · x = Δu	terreno in drenaggio	cedimento primario	Se
t	t ⇒ ∞	u = 0	terreno drenato	cedimento secondario	Ss

 

Cedimento come variazione di volume/spessore 

Cedimento come variazione di volume

Cedimento come variazione di spessore

Cedimento come variazione della porosità/indice dei vuoti

Cedimento come variazione della porosità

Cedimento come variazione dell’indice dei vuoti

Prova edometrica

 

 

Caratteristiche della prova edometrica

Interpretazione delle prova edometrica

Curve cedimento (S_e) _ tensione (σ’)

)Determinazione dei coefficiente di compressibilità (a_v, m_v)

Determinazione della tensione di preconsolidazione (σ’_p ) e degli indici di compressibilità

Utilizzo della curva e_log σ’

MODO 1 – Determinazione della tensione di preconsolidazione (σ’_p )

• Prolungare i due rettilinei della curva e_log σ’
• Il punto di intersezione fra i due tratti rettilinei individua il punto P ed in ordinata avremo la pressione di preconsolidazione σ’_p

MODO 2 – Determinazione della tensione di preconsolidazione secondo Casagrande

σ’_p  (tensione efficace di preconsolidazione)
σ’_{p max}  (tensione efficace di preconsolidazione limite minimo)
σ’_{p min} (tensione efficace di preconsolidazione massimo)
m (retta bisettrice dell’angolo formato da i due rami della curva) (colore grigio)
M (punto di massima curvatura individuato dall’intersezione fra m e la curva edometrica)
t (retta tangente alla curva e passante per M) (colore nero tratteggiata)
o (retta orizzontale passante per M) (colore grigio tratteggiata)
b (retta bisettrice dell’angolo formato da t ed o) (colore rosa)

Determinazione e degli indici di compressibilità (C_r, C_c, C_s)

Utilizzo della curva e_log σ’

σ’_p  (tensione efficace di ricompressione)

retta di  ricompressone (colore verde)
retta di compressione vergine (colore rosso)
retta di rigonfiamento (colore arancione)

Calcolo del cedimento edometrico (S_e)

Formula generale del cedimento edometrico (Se)

Consolidazione edometrica e cedimento – Casi reali

Terreni Normalconsolidati (N.C.)

Terreni Sovraconsolidati (O.C.)

Parametri della consolidazione edometrica a seguito di incremento di carico

GRADO DI CONSOLIDAZIONE EDOMETRICO MONODIMENSIONALE (U)

FATTORE TEMPO (T_v)

Coefficiente di consolidazione edometrico

FATTORE POSIZIONE (Z)

Relazione fra U_z, T_v e Z

Calcolo del tempo di consolidazione edometrica

Interpretazione delle curve S_e_log t e S_e_log t

Curve cedimento (Se) _ tempo (t)

Calcolo del C_v sperimentale (Metodo di Casagrande)

Utilizzo della curva cedimento (S_e_log t) tempo per il calcolo di t₅₀ e c₅₀

Calcolo del tempo di consolidazione dello spessore del terreno

---

STATI TENSIONALI NEL SISTEMA TERRENO

Analisi degli stati tensionali all’interno di un terreno

Condizioni di rottura

Terreni senza coesione

 

Calcolo delle tensioni efficaci per terreni senza coesione 

Terreni con coesione

Calcolo delle tensioni efficaci per terreni con coesione 

---

SPINTA DELLE TERRE

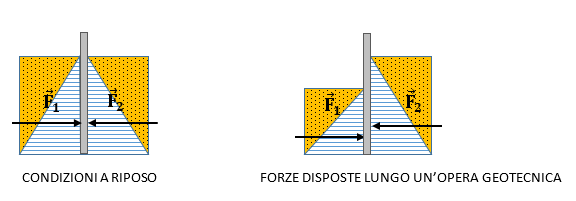
SPINTA A RIPOSO (S₀)

SPINTA ATTIVA (S_A)

Spinta attiva in un terreno senza coesione

Incremento della spinta attiva di un terreno senza coesione su cui è stato posto un sovraccarico Δq

Spinta dell’acqua (terreno senza coesione sottofalda)

Spinta attiva in un terreno con coesione

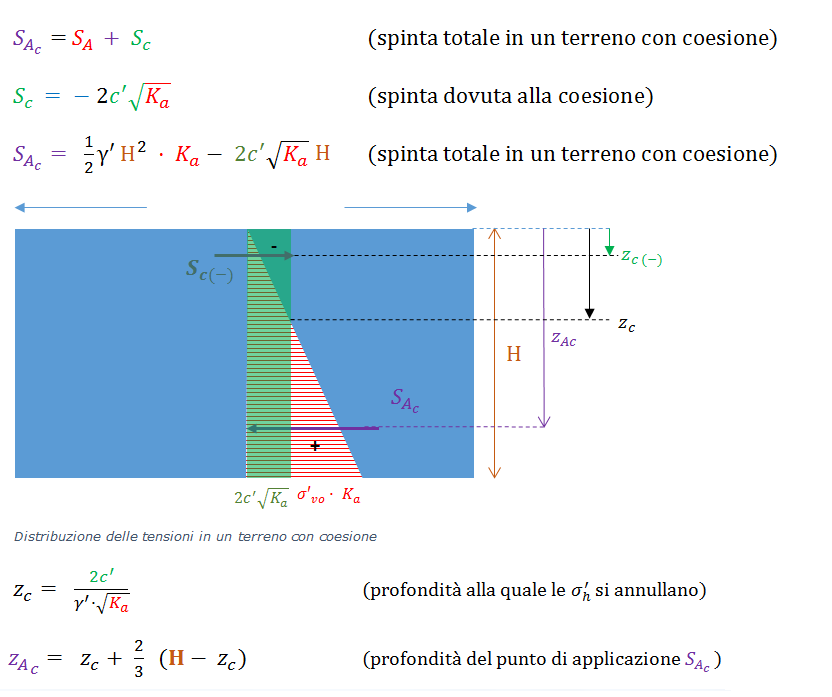
Spinta dovuta alla coesione nel campo negativo

Incremento della spinta attiva di un terreno con coesione su cui è stato posto un sovraccarico Δq

Spinta dell’acqua (terreno con coesione sottofalda)

SPINTA PASSIVA (S_P)

Spinta passiva in un terreno senza coesione

Spinta passiva in un terreno con coesione

Calcolo dei punti di applicazione delle spinte

(sezione in costruzione)

---

CALCOLO DELLE SPINTE AGENTI SU OPERE GEOTECNICHE

OPERE DI SOSTEGNO

• PARATIE
• MURI
• STRUTTURE MISTE

---

PARATIE

PARATIE INFISSE SEMPLICI

Spinte agenti su di una paratia infissa in un terreno con coesione

CASO 1

CONDIZIONI

• P.C. ORTOGONALE ALLA PARATIA
• TERRENO SOPRAFALDA CON COESIONE SU ENTRAMBI I LATI DELLA PARATIA

LATO DX DELLA PARATIA  (CONDIZIONI DI SPINTA ATTIVA)

LATO SX DELLA PARATIA  (CONDIZIONI DI SPINTA PASSIVA)

CASO 2

CONDIZIONI

1) P.C. NON ORTOGONALE ALLA PARATIA  SUL LATO DX DELLA PARATIA

2) TERRENO SOPRAFALDA CON COESIONE SU ENTRAMBI I LATI DELLA PARATIA

LATO DX DELLA PARATIA  (CONDIZIONI DI SPINTA ATTIVA)

Le spinte vanno considerate vettorialmente, quindi considerando la pendenza del P.C. (β) rispetto alla paratia

CASO 3

CONDIZIONI (APPLICAZIONE DELLA TEORIA DI COULOMB)

1) P.C. NON ORTOGONALE ALLA PARATIA SU ENTRAMBI I LATI 
2) PARATIA INCLINATA 
3) TERRENO SOPRAFALDA SENZA COESIONE 

LATO DX

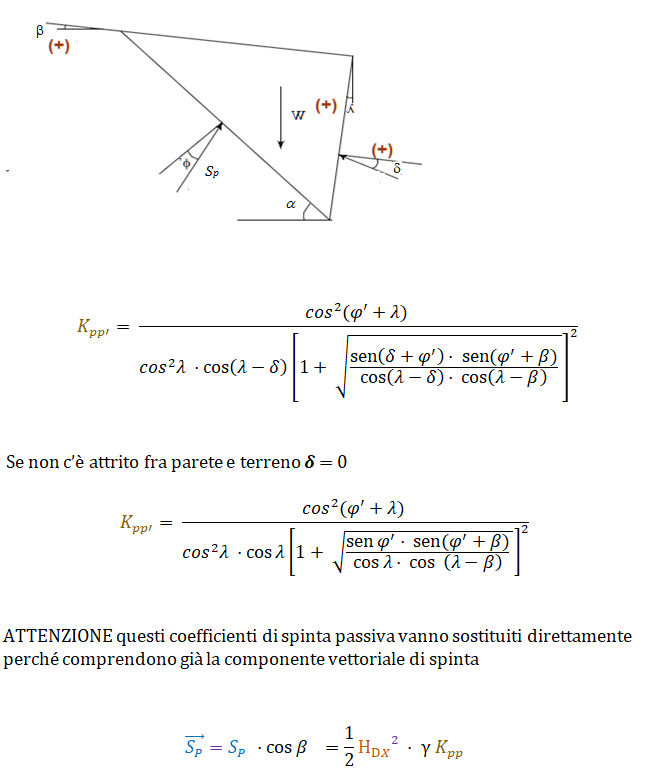
Spinta attiva in terreno senza coesione con pendenza e con parete inclinata sulla verticale di un angolo λ (Teoria di Coulomb) in presenza di attrito parete terreno con coefficiente d’attrito tg 𝜹

Distribuzione delle forze su paratia inclinata – lato DX

ATTENZIONE: questi coefficienti di spinta attiva vanno sostituiti direttamente alla formula per il calcolo della spinta perché comprendono già la componente vettoriale di spinta

LATO SX

Spinta passiva  in terreno senza coesione con pendenza e con parete inclinata sulla verticale di un angolo λ (Teoria di Coulomb) in presenza di attrito parete terreno con coefficiente d’attrito tg 𝜹

CASO 4

CONDIZIONI (APPLICAZIONE DELLA TEORIA DI COULOMB)

1) P.C. NON ORTOGONALE ALLA PARATIA
2) PARATIA INCLINATA CON ATTRITO E ADESIONE PARETE TERRENO
3) TERRENO SOPRAFALDA CON COESIONE 

Calcolo della spinta attiva

 

Calcolo della spinta attiva dovuta alla sola coesione del terreno

Calcolo della spinta dovuta all’adesione muro-terreno

Attenzione: spesso nei calcoli dei coefficienti di sicurezza questo valore è trascurato

Calcolo di Z_c

Calcolo del modulo della spinta dovuta all’adesione muro-terreno

Spinta totale attiva su terreno dotato di coesione in attrito con la parete di sostegno

Verifica SLU per le PARATIE – DM 17.1.2018

	APP1		APP2
	C1	C2	C*
AZIONI	A1	A2	A1
PARAMETRI GEOTECNICI	M1	M2	M1
RESISTENZE	R1*	R1*	R3

 

 

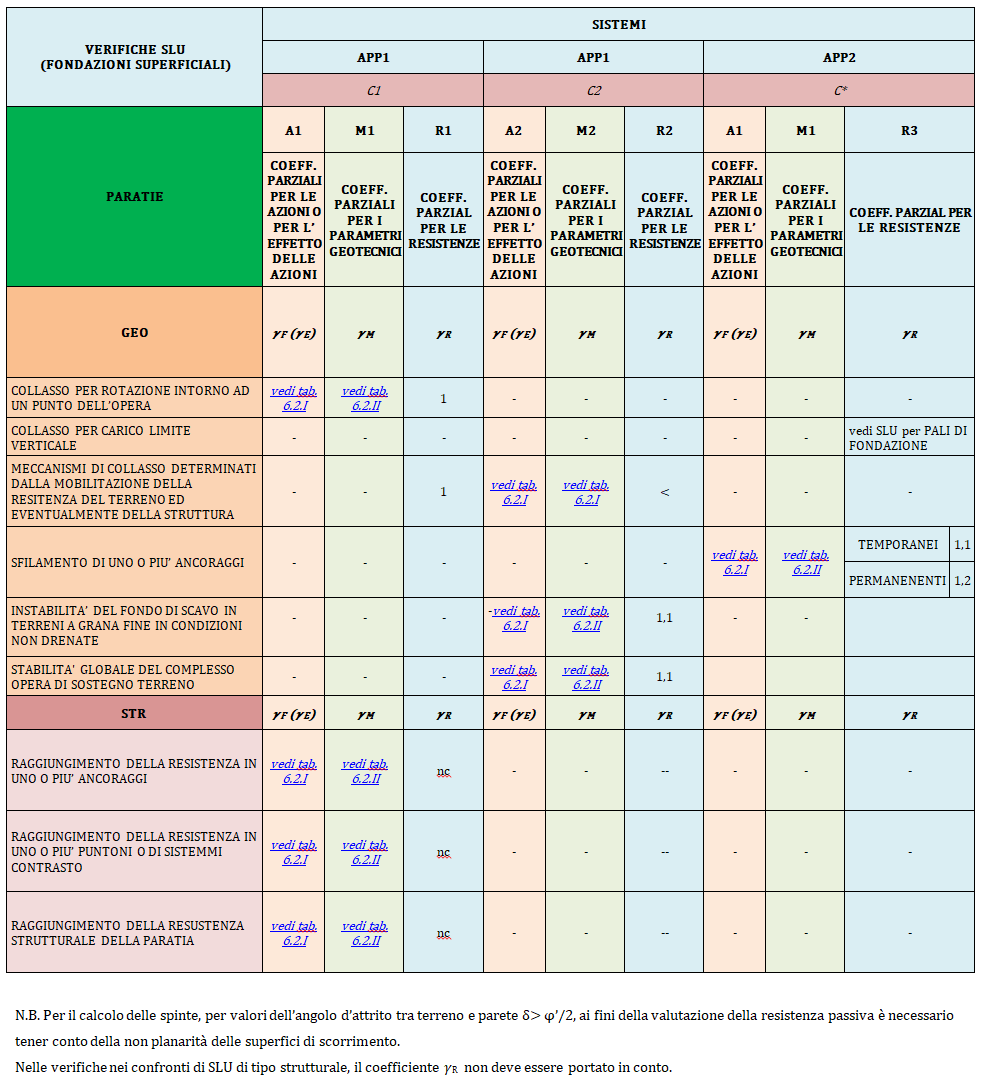
Coefficienti di spinta in condizioni sismiche

Metodo di Caquot e Kerisel

Coefficiente di spinta attiva 

 

r = 2 (per opere che prevedano spostamenti o che siano sufficientemente flessibili
r = 1 nel caso di terreni coesivi saturi dominanti
per opere con H < 10 m i coefficienti si possono assumere costanti lungo l’altezza del muro

Coefficiente di spinta passiva 

Metodo di Mononobe-Okabe

per a_g, F₀, T^*vedere  dm-14-01-2008_tabella-1 e dm-14-01-2008_tabella-2 – (All. A/B DM 14.1.2008)

Coeff. di spinta attiva/passiva secondo Mononobe-Okabe

Coefficiente di spinta attiva (MO)

Coefficiente di spinta passiva (MO)

Inclinazione del piano di scorrimento (MO)

 

*** sezione in costruzione ***

Incremento di spinta sismica

ΔS =  S_a–S_a’ 

S_a spinta in condizioni statiche
S_a’ spinta in condizioni dinamiche

Muri di sostegno

Classificazione in base al posizionamento dell’opera da proteggere

• Muri di sostegno di controripa (o in sterro)
  Muri di sostegno in rilevato (o di sottoscarpa)

Classificazione in base alla tipologia di muro

• • Muri di sostegno a gravità
  • Muri di sostegno elastici
  • Muri di sostegno a contrafforti e speroni

Classificazione in base alla forma del muro

• Muri rettangolari
• Muri ad una scarpa
• Muri a doppia scarpa
• Muri a gradoni
  • esterni
  • interni

Elementi fondamentali del muro

 

Verifiche di sicurezza al ribaltamento per muri di sostegno (senza sbalzo alla fondazione)

 

Verifiche di sicurezza alla traslazione per muri di sostegno (senza sbalzo alla fondazione)

Verifica agli stati limite ultimi (SLU) per muri di sostegno

SLU per muri di sostegno – verifiche al ribaltamento

VERIFICA SLU – GEO – APPROCCIO 2 – A1- M1 – R3

	APP1		APP2
	C1	C2	C*
AZIONI	A1	A2	A1
PARAMETRI GEOTECNICI	M1	M2	M1
RESISTENZE	R1*	R2	R3

 

CASO 1

Combinazione delle azioni senza la presenza di sovraccarichi

• azioni (vedi tab. 6.2.I – D.M. 17.01.2018)  – G1 (carichi permanenti)

Ed (totale delle azioni)  = M_s (momento della spinta del terreno)

Carichi permanenti G1

• Spinta delle terre (S_t)
  • si calcola valore della spinta totale agente sul muro (S_t)
  • si applica il coefficiente di correzione (vedi tab. 6.2.I – D.M. 17.01.2018) per l’azione SFAVOREVOLE esercitata dal terreno rispetto al RIBALTAMENTO
  • la colonna A1 prevede un γ_G1 = 1,3
  • il valore calcolo (S_d) per la spinta delle terre sarà dato da:

S_d = S_t · γ_G1

• Calcolo del momento della spinta totale S_t (M_S)

CASO 2 – Combinazione delle azioni in presenza di sovraccarichi

• azioni (vedi tab. 6.2.I – D.M. 17.01.2018)  – G1 (carichi permanenti) + Q (azioni variabili)

E_d = M_s + M_q

E_d (totale delle azioni)
M_s (momento della spinta del terreno)
M_q (momento della spinta del sovraccarico)

Carichi permanenti G1

• Spinta delle terre (S_t)
  • vedi CASO 1

• Calcolo del momento della spinta totale S_t (M_S)
  • vedi CASO 1

Azioni variabili (Q)

• Spinta dovuta al sovraccarico (S_q)
  • si calcola valore della spinta sul muro dovuta al sovraccarico (S_q)
  • si applica il coefficiente di correzione (vedi tab. 6.2.I – D.M. 17.01.2018) per AZIONI VARIABILI – SFAVOREVOLE esercitata dal sovraccarico rispetto al RIBALTAMENTO
  • la colonna A1 prevede un γ_Q = 1,5
  • il valore di calcolo (S_q) per la spinta dovuta al sovraccarico sarà dato da:

S_dq = S_q · γ_Q

• Calcolo del momento della spinta dovuta al sovraccarico S_q (M_q)

Determinazione delle resistenze 

• parametri geotecnici del terreno (vedi tab. 6.2.II – D.M. 17.01.2018) – M1
• coefficienti di resistenza (vedi tab. per muri di sostegno) – R3

Parametri geotecnici (vedi Tab. 6.2.II – D.M. 17.01.2018)

TIPOLOGIA	DESCRIZIONE PARAMETRO	PARAMETRO GEOTECNICO DEL TERRENO	COEFF.	CASI
		xk	γM	(M1)	(M2)
TERRENI A STRUTTURA SEMPLICE	TANGENTE DELL’ANGOLO DI RESISTENZA	tan φ’k	γφ’	1,00	1,25
	PESO DELL’UNITA’ DI VOLUME	γ	γγ	1,00	1,00
	COESIONE EFFICACE	c’k	γc’k	1,00	1,25
	COESIONE NON DRENATA	cu	γcu	1,00	1,00
TERRENI A STRUTTURA COMPLESSA o AMMASSI ROCCIOSI	VALORE CARATTERISTICO DELLA RESISTENZA UNITARIA AL TAGLIO	τR	γτR	1,00	1,25

 

Determinazione del valore di calcolo

x_{k /} γ_M 

γ_M  (coefficiente parziale secondo tabella)
x_k (parametro geotecnico del terreno)

• in questo caso bisogna considerare i fattori correttivi M1, essendo tutti pari a 1, i valori di calcolo corrisponderanno ai valori caratteristici

Determinazione delle resistenze (R_d)

Combinazione delle azioni resistenti

• azioni (vedi tab. 6.2.I – D.M. 17.01.2018)  – G1 (carichi permanenti)

R_d (totale delle azioni resistenti)  = M_A (momento resistente dovuto al muro)

Carichi permanenti G1

• Peso proprio del muro (W)
  • si calcola il valore del peso di ciascun elemento del muro considerando il suo baricentro (W₁ + W₂) come nella sezione precedente
  • si applica il coefficiente di correzione (vedi tab. 6.2.I – D.M. 17.01.2018) per l’azione FAVOREVOLE esercitata dal peso del muro che si oppone al RIBALTAMENTO
  • la colonna A1 prevede un γ_G1 = 1
  • il valore di calcolo di (W_d) per ciascun elemento di muro (i) sarà dato da:

W_di = W_i · γ_G1

ovvero

W_di = W_i 

essendo γ_G1 = 1

• Calcolo dei momenti dovuti al peso proprio dei vari elementi del muro W (M_Ai) che 

M_A = M_A1 + M_A2 (momento resistente totale)

Rd di calcolo e coefficiente parziale 

Rd = M_A1 + M_A2

dove Rd* rappresenta il valore di calcolo delle azioni resistenti.

• γ_R = 1,15 come previsto nella tabella per le verifiche SLU per muri di sostegno alla colonna R3 nella verifica al ribaltamento

 Verifica al ribaltamento

E_d = M_s + M_q  (caso con sovraccarico)

R_d* = M_A/1,5

Ed ≤ R_d*

ovvero

M_s + M_q ≤ R_d*

SLU per muri di sostegno – Verifiche allo scorrimento

VERIFICA SLU – STR – A1- M1 – R13 (vedi Tab. 6.2.I – D.M. 17.01.2018)

	C*
AZIONI	A1
PARAMETRI GEOTECNICI	M1
RESISTENZE	R3*

 

*per la verifica allo SCORRIMENTO

Verifica sul piano del MURO

CASO 1

Combinazione delle azioni senza la presenza di sovraccarichi

• azioni (vedi tab. 6.2.I – D.M. 17.01.2018)  – G1 (carichi permanenti)

Ed (totale delle azioni)  = S_t (spinta del terreno)

Carichi permanenti G1

• Spinta delle terre (S_t)
  • si calcola valore della spinta totale agente sul muro (S_t)
  • si applica il coefficiente di correzione (vedi tab. 6.2.I – D.M. 17.01.2018) per l’azione SFAVOREVOLE esercitata dal terreno rispetto allo SCORRIMENTO
  • la colonna A1 prevede un γ_G1 = 1,3
  • il valore calcolo (S_d) per la spinta delle terre sarà dato da:

S_d = S_t · γ_G1

CASO 2 – Combinazione delle azioni in presenza di sovraccarichi

• azioni (vedi tab. 6.2.I – D.M. 17.01.2018)  – G1 (carichi permanenti) + Q (azioni variabili)

E_d = S_t + S_q

E_d (totale delle azioni)
S_q (spinta sul muro dovuta al sovraccarico)

Carichi permanenti (G1)

• Spinta delle terre (S_t)

Azioni variabili (Q)

• Spinta dovuta al sovraccarico (S_q)
  • si calcola valore della spinta sul muro dovuta al sovraccarico (S_q)
  • si applica il coefficiente di correzione (vedi tab. 6.2.I – D.M. 17.01.2018) per AZIONI VARIABILI – SFAVOREVOLE esercitata dal sovraccarico rispetto allo SCORRIMENTO
  • la colonna A1 prevede un γ_Q = 1,5
  • il valore di calcolo (S_q) per la spinta dovuta al sovraccarico sarà dato da:

S_dq = S_q · γ_Q

Determinazione delle resistenze 

• parametri geotecnici del terreno (vedi tab. 6.2.II – D.M. 17.01.2018) – M1
• coefficienti di resistenza (vedi tab. per muri di sostegno) – R3

Parametri geotecnici (vedi Tab. 6.2.II – D.M. 17.01.2018)

TIPOLOGIA	DESCRIZIONE PARAMETRO	PARAMETRO GEOTECNICO DEL TERRENO	COEFF.	CASI
		xk	γM	(M1)	(M2)
TERRENI A STRUTTURA SEMPLICE	TANGENTE DELL’ANGOLO DI RESISTENZA	tan φ’k	γφ’	1,00	1,25
	PESO DELL’UNITA’ DI VOLUME	γ	γγ	1,00	1,00
	COESIONE EFFICACE	c’k	γc’k	1,00	1,25
	COESIONE NON DRENATA	cu	γcu	1,00	1,00
TERRENI A STRUTTURA COMPLESSA o AMMASSI ROCCIOSI	VALORE CARATTERISTICO DELLA RESISTENZA UNITARIA AL TAGLIO	τR	γτR	1,00	1,25

 

Determinazione del valore di calcolo

x_{k /} γ_M 

γ_M  (coefficiente parziale secondo tabella)
x_k (parametro geotecnico del terreno)

• in questo caso bisogna considerare i fattori correttivi M1, essendo tutti pari a 1, i valori di calcolo corrisponderanno ai valori caratteristici

Determinazione delle resistenze (R_d)

Combinazione delle azioni resistenti

• azioni (vedi tab. 6.2.I – D.M. 17.01.2018)  – G1 (carichi permanenti)

R_d (totale delle azioni resistenti)  = W_M (peso totale del muro)

Carichi permanenti G1

• Peso proprio del muro (W)
  • si calcola il valore del peso di ciascun elemento del muro considerando il suo baricentro (W₁ + W_{2+ …} ) come nella sezione precedente
  • si applica il coefficiente di correzione (vedi tab. 6.2.I – D.M. 17.01.2018) per l’azione FAVOREVOLE esercitata dal peso del muro che si oppone allo SCORRIMENTO
  • la colonna A1 prevede un γ_G1 = 1
  • il valore di calcolo di (W_dM) per ciascun elemento di muro (i) sarà dato da:

W_di = W_i · γ_G1 

ovvero

W_di = W_i 

essendo γ_G1 = 1

W_{dM = Σ}W_di  (peso totale di calcolo del muro)

N.B. Se si vuole verificare lo scorrimento sul piano di posa del sistema muro-fondazione, nel calcolo si dovrà considerare anche il peso della fondazione

R_d di calcolo e coefficiente parziale 

• γ_R = 1,1 come previsto nella tabella per le verifiche SLU per muri di sostegno alla colonna R3 nella verifica al ribaltamento 

---

Stabilità dei pendii

CONDIZIONI – Pendio infinito

CASO A  – falda inclinata rispetto al P.C. – Assenza di filtrazione all’interno del terreno

CASO 1 – c’ = 0, u = 0 – falda molto al di sotto del P.C.

 

CASO 2 – c’ = 0, u ≠ 0, falda al di sopra del P.C. – assenza di filtrazione attraverso il terreno 

CASO B  – falda parallela ed al di sotto rispetto al P.C. – presenza di filtrazione all’interno del terreno

CASO 1 – c’ = 0, u ≠ 0,  falda al di sotto del P.C. 

CASO 2 – c’ = 0, u ≠ 0, falda coincidente al P.C. (m=1)

CASO 3 – c’ = 0, u ≠ 0, falda alla base dell’elemento di terreno considerato (m < 0)

se c’≠ 0 basterà aggiungere c’ al numeratore in tutti i casi esposti

*** sezione in costruzione ***

---

Stabilità dei pendii artificiali (fronti di scavo)

Metodo di Culmann

Sistema semplice a cuneo singolo

Sistema a doppio cuneo 

 

Forza normale agente sul CUNEO 1 (N₁) fattore di sicurezza  (FS)

Forza normale agente sul CUNEO 2 (N₂) fattore di sicurezza (FS)

Si procederà per tentativi per la determinazione del FS assumendo θ = φ_max.

---

Stabilità dei pendii (superfici non piane)

Metodo di Taylor

c_u≠ 0 (coesione in condizioni non drenate)

*** sezione in  costruzione ***

---

Capacità portante delle fondazioni superficiali

Equazione generale di capacità portante di fondazioni superficiali

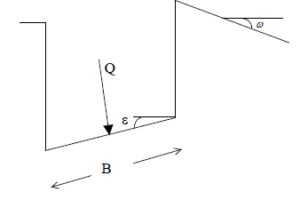
Fondazione nastriforme con carico verticale centrato

c’ ≠ 0

Analisi del carico limite (q_lim) in termini di tensioni totali

CONDIZIONI NON DRENATE – TERRENI A GRANA FINE

Verifiche SLU – NTC 2018

*** SEZIONE IN COSTRUZIONE ***