sezione in costruzione (-50 trucchi) aggiornato al 19.07.2022

Il concetto che sta alla base di qualsiasi trucco matematico è quello di semplificare un problema in problemi più piccoli e più semplici da risolvere. Di seguito vengono proposti i più conosciuti trucchi matematici (ne esistono diversi altri) divisi per tipologia di operazione da effettuare. L’obiettivo è quello di diminuire il tempo di risposta, facendo calcoli a mente e senza far ricorso alla calcolatrice.

INDICE 

1. ADDIZIONE (O SOMMA)

2. SOTTRAZIONE O (DIFFERENZA)

3. MOLTIPLICAZIONE (O PRODOTTO)

4. QUADRATI

        1. QUADRATI DI NUMERI DA 42 a 59
        2. QUADRATI DI NUMERI DA 92 a 109

5. RADICI

6. DIVISIONE (O QUOZIENTE) 

7. COME RICAVARE FORMULE INVERSE

8. EQUAZIONI ED ESPRESSIONI

    9. PERCENTUALI e FRAZIONI

      • CALCOLO DI PERCENTUALI (TRUCCO 44)
      • CONFRONTO TRA FRAZIONI (TRUCCO 45)

   10. TRUCCHI CONTABILI

      •  SCORPORO DELL’IVA (TRUCCO 46)

   11. FISICA-MATEMATICA

      • CONVERSIONE CELSIUS (°C) ⇔ FAHRENHEIT (°F) (TRUCCO 47)
      • CONVERSIONE CELSIUS (°C) ⇔ KELVIN (°K) (TRUCCO 48)

12. GEOMETRIA

  • INDIVIDUAZIONE DELLE COORDINATE DI UNA RETTA PER DISEGNARLA (TRUCCO 49)

13. ALTRI TRUCCHI

  • GIORNI DELLA SETTIMANA (TRUCCO 50)

#

1) ADDIZIONE O SOMMA

#

(TRUCCO 1) SOMMA DI PIÙ DI DUE ADDENDI

Es 1) Se dobbiamo sommare, 15+6+9+21+15+24.

PASSO 1) Cominciamo a sommare i termini a due a due:

PRIMO ACCOPPIAMENTO

15+6=21 (prima coppia); 9+21=30 (seconda coppia) ; 15+24= 39 (terza coppia)

SECONDO ACCOPPIAMENTO

21+30 = 51

PASSO 2) Rimane fuori dall’accoppiamento successivo il 39 che andremo a sommare alla prima coppia frutto del secondo accoppiamento

E così alla fine 51+39 = 90

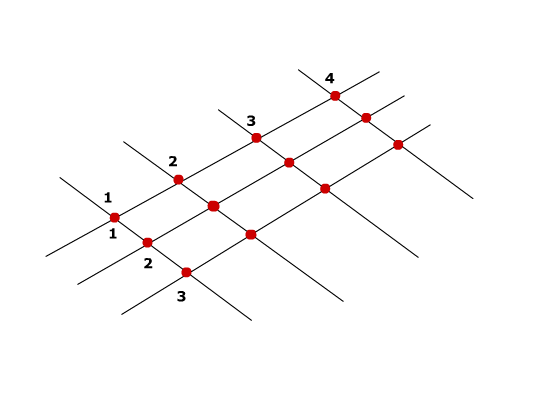
Questi passaggi possono essere effettuati anche con un metodo grafico. Consiglio questo:
ponete su una riga tutti gli addendi e procedete per somme parziali come nell’esempio

#

(TRUCCO 2) SOMMA PER ARROTONDAMENTO

Es 1) 72 + 14

72+8 = 80 (arrotondamento)

80 + 14 = 94

94 – 8 = 86

#

(TRUCCO 3) SOMMA DA SINISTRA

Es 1) 5678 + 76 = 5754

Es 2) 5973 + 2791 = 8764

Es 3) 6897  + 5678 = 12575

Passo 1 – Si procede sommando da sinistra le prime cifre dei due numeri. La somma si effettua controllando se la somma delle due cifre immediatamente a destra è maggiore di 10. Questa somma può essere al massimo compresa fra 11 e 19.  Se si verifica questo caso la somma ottenuta dovrà essere aumentata di 1.

Passo 2 – Si procede in questo modo tenendo conto dei riporti successivi

#

(TRUCCO 4)  SOMMA DI DUE NUMERI REALI

  • Se il segno è uguale
    1. Sommare i due numeri e mettere davanti lo stesso segno che hanno i due numeri
  • Se il segno è diverso
    1. Sottrarre i due numeri e mettere davanti il segno del numero più grande

#

SOMMA DI NUMERI RAZIONALI

#

CASO 1 – Somma di un numero intero più un numero razionale. (TRUCCO 5) 
1) Il denominatore D sarà dato dal denominatore della frazione che stiamo sommando
2) il numeratore N sarà dato dal prodotto del denominatore per il numero intero sommato al numeratore della frazione

Es 1)

⇒ D = 4
⇒ N = 5 + (2 x 4) = 13 

#

CASO 2 – Somma di un numero razionale con 1 (TRUCCO 6) 

  • Il denominatore D sarà dato dal denominatore della frazione che stiamo sommando
  • I numeratore N sarà dato dalla somma di numeratore e denominatore della frazione che stiamo sommando

Es 1)

#

CASO 3 – Somma di due numeri razionali con numeratore uguale a 1 e denominatori (D1 e D2) numeri primi (TRUCCO 7)

SOLUZIONE

#

(TRUCCO 8) CASO 4 – Somma di due numeri razionali il cui denominatori (D1 e D2) sono numeri primi oppure solo uno dei due denominatori è un numero primo non sottomultiplo dell’altro.

SOLUZIONE

#

2) SOTTRAZIONE (o DIFFERENZA)

#

(TRUCCO 9) SOTTRAZIONE PER ARROTONDAMENTO

ES 1) 256 – 194

194+6 = 200 (arrotondamento)

256 – 200 = 56

56 + 6 = 62

#

(TRUCCO 10) SOTTRAZIONE DA 1000

MODO 1

ES 1) 1000 – 477 = 523

9-4 = 5
9-7 = 2
10-7 = 3

MODO 2

Un altro modo per risolvere velocemente la differenza da 1000 è quello che considera che le cifre prese ad una ad una del numero da sottrarre deve dare come risultato 9 tranne l’ultima che deve dare 10. Prendendo lo stesso esempio del MODO 1, abbiamo 4 per le centinaia quindi il primo numero sarà 5, per le decine è 7 , quindi il secondo numero sarà 2, mentre per le unità abbiamo 7 e così, poiché la somma deve dare 10, il terzo numero sarà 3.

#

3) MOLTIPLICAZIONE (o PRODOTTO)

#

(TRUCCO 11) MOLTIPLICARE UN NUMERO AD UNA CIFRA PER UN NUMERO A DUE CIFRE MAGGIORE DI 10

  1. Moltiplicare il numero ad una sola cifra per le decine del numero a due cifre e moltiplicarlo per 10
  2. Sommare il numero ottenuto dal prodotto delle unità al numero ottenuto nella (1.)

Es. 1) 7 x 29  ⇒ 7×2 = 14  ⇒  14×10 = 140 poi 7×9 = 63 ⇒ 140+63 = 203

#

(TRUCCO 12) MOLTIPLICARE UN NUMERO AD UNA CIFRA PER 11, 111, 1111, ecc..

Ripetere il numero

Es. 1) 7×11 = 77

Es 2) 8×111 = 888

#

(TRUCCO 13) MOLTIPLICAZIONE DI UN NUMERO A DUE CIFRE PER 11

a. Il numero delle unità del numero che dobbiamo ottenere è identico al numero delle unità del numero che stiamo moltiplicando per 11.

b. Il numero di decine del numero che dobbiamo ottenere è dato dalla somma delle cifre del numero che stiamo moltiplicando

      1. Se la cifra è un numero maggiore di 10 scriviamo il numero delle unità e consideriamo il riporto

c. Il numero delle centinaia sarà identico al numero delle decine del numero che stiamo moltiplicando sommato al riporto se ci troviamo nel caso b1

Es. (1)      11×52 ⇒ 5 (centinaia) 5+2 = 7 (decine) 2 (unità) ⇒ 572

Es. (2)      11×84 ⇒ 8 (centinaia) 8+4 = 12 (1 centinaia e 2 decine) 4 (unità) ⇒

8+1 2  4  ⇒ 924

#

(TRUCCO 14) MOLTIPLICAZIONE DI UN NUMERO  A DUE CIFRE PER 12 

Moltiplicare per 10 e poi aggiungere il numero moltiplicato per 2

Es. 56 x 12 ⇒ 56 x 10 = 560 ⇒ 56 x 2 = 112  ⇒ 560+112=672

#

(TRUCCO 15) MOLTIPLICAZIONE A DUE CIFRE 

a1 b1 x a2 b2

dove a1 (valore della decina del primo numero)
b1 (valore della unità del primo numero)
a2 (valore della decina del secondo numero)
b2 (valore dell’unità del primo numero)

SOLUZIONE

mc =  a1 x a2    d = (a1 x b2)+ (a2 x b1)  u = b1 x b2 

(N.B.  E’ necessario ovviamente considerare i riporti)

Es 1) 43 x 52 ⇒ mc =  4 x 5    d = (4 x 2)+ (5 x 3)  u = 3x2

⇒20  23 6 ⇒ 2236

#

(TRUCCO 16) CASO 1 – b1 = b2 = 1

a1 1   x  a2 1

SOLUZIONE

c = a1 x a2    d = a1+ a2    u =1

cdu

N.B le decine debbono essere riportate se d = a1 + a2    > 10

Es 51 x 41 ⇒ a1 = 5, a2 = 4,  b1 = b2 = 1

51   x  41

mc = 5 x 4    d = 5 + 4    u = 1

20    9    1  ⇒ 2091

#

(TRUCCO 17) CASO 2 – b1 = b2 = 2 

a1 2   x  a2 2

SOLUZIONE

mc = a1 x a2    d = (a1+ a2) x2    u =(2×2)

mcdu

N.B le decine debbono essere riportate se d = a1 + a2    > 10

Es 52 x 42 ⇒  a1 = 5, a2 = 4,  b1 = b2 = 2

52  x  42

mc = 5 x 4    d = (5 + 4) x 2    u = 4

20    18   1  ⇒ 2184

#

(TRUCCO 18) CASO 3 – b1 = b2 = 3 

a1 3  x  a2 3

SOLUZIONE

mc = a1 x a2    d = (a1+ a2) x 3    u = (3×3)

mcdu

N.B le decine debbono essere riportate se d = a1 + a2 > 10

Es 53 x 43   a1 = 5, a2 = 4, b1 = b2 = 3

53 x 43

c = a1 x a2    d = (a1+ a2) x3    u = (3×3)

20   27   9 ⇒ 2279

#

(TRUCCO 19) CASO 4  b1 = b2 = 4 

a1 4  x  a2 4

SOLUZIONE

mc = a1 x a2    d = (a1+ a2) x 4    u = (4×4)

mcdu

N.B le decine debbono essere riportate

Es 54 x 44  ⇒ a1 = 5, a2 = 4, b1 = b2 = 4

53 x 43

mc = 5 x 4    d = (5+4) x 4    u = (4×4)

20   36   16 ⇒ 2376

#

(TRUCCO 20) CASO 5     a1 = a2 = a   e b1 + b2 = 10 

a b1   x  a b2

SOLUZIONE

mc = a x (a+1)  u = b1 x b2  

Es. 1) 43 x 47 ⇒  a = 4, b2 = 3, b2 = 7

mc =  4 x (4+1)   du = 3 x 7   = 21

20  21 ⇒ 2021

#

(TRUCCO 21) CASO 6  –  a1 = a2 = 1   

1b1   x   1b2

SOLUZIONE

cd = (1 b1   +    b2  ) x 10

u = b1   x   b2

c+du = cdu

ES .  13 x 17   a = 1, b1 = 3, b2 =  7

c = (13 + 7)  x 10 = 200

 du = 3 x 7   = 21

RISULTATI: 200 +   21 ⇒ 221

#

(TRUCCO 22) CASO 7  –  a1 = a2 > 1÷9

ab1   x   ab2

SOLUZIONE

cdu = [(ab1   +    b2)x a] x 10

u = (b1   x   b2)

c+du = cdu

ES .  23 x 27   a = 2, b1 = 3, b2 =  7

c = [(23 + 7)x2] x 10 = (30×2) x10 = 600

 du = 3 x 7   = 21

RISULTATO: 600 +   21 ⇒ 621

#

(TRUCCO 23) MOLTIPLICAZIONE DI DUE NUMERI COMPRESI FRA 51 e 99

SOLUZIONE

PASSO 1) Stabilire la distanza da 100

PASSO 2) Sommando le differenze da 100 e poi sottraendo il risultato da 100 si ottengono le prime due cifre

PASSO 3) Moltiplicando le differenze da 100 si ottengono le ultime due cifre

Es. 1) 85 x 87

100-85 = 15 ⇒ 100-87 = 13 (PASSO 1)

15+13 = 28 ⇒ 100-28 = 72 (PASSO 2)

15 x 13 = 1(PASSO 3)

Tenendo conto anche dei riporti si ottiene 7395 

#

(TRUCCO 24) MOLTIPLICAZIONE DI UN NUMERO PER 5, 50, 500, ecc.

  • Moltiplicazione per 5 – dividere il numero per 2 e moltiplicarlo per 10
  • Moltiplicazione per 50 – dividere il numero per 2 e moltiplicarlo per 100
  • Moltiplicazione per 500 – dividere il numero per 2 e moltiplicarlo per 1000

Es 1) 50 x 24 ⇒ 24:2 = 12 ⇒ 12 x 100 = 1200

Es 2) 500 x 16  ⇒ 16:2 = 8 ⇒ 8 x 1000 = 8000

#

(TRUCCO 25) MOLTIPLICAZIONE DI UN NUMERO PER 9, 90, 900, ecc.

PASSO 0 – Scrivere la seguente tabella oppure tenerla a mente

1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 10

PASSO 1

CASO 1 

La prima cifra del numero da moltiplicare è minore di quella del secondo.

PASSO 1

Riscrivere la prima cifra del numero da moltiplicare sarà la prima cifra del numero del risultato.

PASSO 2

Calcolare quanti numeri ci sono fra la prima cifra e la seconda cifra del numero che deve essere moltiplicato per 9.

PASSO 3

Calcolare quanti numeri ci sono a destra della seconda cifra compreso 10

ES. 79 x 9

PASSO 1

Riscriviamo la prima cifra, 7. Questo numero sarà la prima cifra del risultato.

PASSO 2

Calcoliamo i numeri che ci sono fra 7 e 9. Otteniamo 1, che sarà seconda cifra del risultato. 

PASSO 3

Calcoliamo quanti numeri ci sono dalla seconda cifra a 10. In questo caso 1. Questo numero sarà la terza cifra  del risultato.

SOLUZIONE

711

CASO 2 

La prima cifra del numero da moltiplicare è maggiore di quella del secondo.

PASSO 1

Sottrarre la prima cifra del numero da moltiplicare. il numero così ottenuto sarà la prima cifra del numero del risultato.

PASSO 2

Calcolare quanti numeri ci sono fra la prima cifra e la seconda cifra del numero che deve essere moltiplicato per 9, partendo però dalla cifra più grande e spostandosi verso destra e ricominciando la scala (VEDI PASSO 0) se necessario.

PASSO 3

Calcolare quanti numeri ci sono a destra della seconda cifra compreso 10

ES. 83 x 9

PASSO 1

Sottraiamo 1 alla prima cifra. Questo numero sarà la prima cifra del risultato.

8-1 = 7

PASSO 2

Calcoliamo i numeri che ci sono fra 8 e 3 partendo da 8 ed andando verso destra e ricominciando la scala. Otteniamo 4, che sarà la seconda cifra del risultato. 

PASSO 3

Calcoliamo quanti numeri ci sono fra 3 e 10. In questo caso 7. Questo numero sarà la terza cifra  del risultato.

SOLUZIONE

83 x 9 = 747

#

(TRUCCO 26) MOLTIPLICAZIONE DI UN NUMERO PER 25, 250, 2500, ecc.

  • Moltiplicazione per 25 – dividere il numero per 4 e moltiplicarlo per 100
  • Moltiplicazione per 250 – dividere il numero per 4 e moltiplicarlo per 1000
  • Moltiplicazione per 2500 – dividere il numero per 4 e moltiplicarlo per 10000

Es 1) 92 x 25 ⇒ 92:4 = 23 ⇒ 23 x 100 = 2300

Es 2) 440 x 250 ⇒ 440:4 = 110 ⇒ 110 x 1000 = 110000

#

(TRUCCO 27) MOLTIPLICAZIONE DI UN NUMERO PER 75, 750, 7500, ecc. 

  • Moltiplicazione per 25 – dividere il numero prima per 4 ed aggiungerlo alla sua metà, poi moltiplicarlo per 100
  • Moltiplicazione per 250 – dividere il numero prima per 4 ed aggiungerlo alla sua metà, poi moltiplicarlo per 1000
  • Moltiplicazione per 2500 – dividere il numero prima per 4 ed aggiungerlo alla sua metà, poi moltiplicarlo per 10000

Es 1) 92 x 75 ⇒ 92:4 = 23 ⇒ 92:2 = 46 ⇒ (23 + 46) x 100 = 6900

Es 2) 440 x 750 ⇒ 440:4 = 110 ⇒ 440:2 = 220 ⇒ (110 + 220) x 1000 = 330.000

#

(TRUCCO 28) MOLTIPLICAZIONE DI DUE NUMERI A PIU’ DI DUE DUE CIFRE 

CASO 1 –  Numero a più di due cifre moltiplicato per uno a due cifre

PASSO 1

MOLTIPLICARE OGNI CIFRA del NUMERO a più di due cifre, partendo da destra verso sinistra ovvero dalla cifra delle unità, con il numero a due cifre

Si otterrà di volta in volta un numero a due o tre cifre composto da unità, decine o centinaia. La cifra delle unità andrà riportata nel risultato come ultima cifra a destra, mentre la cifra delle decine (oppure il numero composto dalla cifra delle decine e dalle centinaia) va sommata all’operazione di moltiplicazione successiva.

ESEMPIO

#

4. QUADRATI

#

QUADRATI DI NUMERI DA 42 a 59

#

1.Il numero è minore di 50 (TRUCCO 29)

      • PASSO 1 – Stabilire la distanza del numero 50
      • PASSO 2 – Sottrarre il numero ottenuto da 25, otteniamo così le prime due cifre del risultato
      • PASSO 3 – Il quadrato del numero sottratto sarà l’ultima cifra del risultato (ovviamente è necessario considerare i riporti)

#

2. Il numero è maggiore di 50 (TRUCCO 30)

      • PASSO 1 – Stabilire la distanza del numero 50
      • PASSO 2 – Sommare il numero ottenuto a 25, otteniamo così le prime due cifre del risultato
      • PASSO 3 – Il quadrato del numero aggiunto sarà l’ultima cifra del risultato

#

2. QUADRATI DI NUMERI DA 92 a 109

#

    1. Il numero è minore di 100 (TRUCCO 31)
      • PASSO 1 – Stabilire la distanza del numero 100
      • PASSO 2 – Sottrarre il numero ottenuto da 100, otteniamo così le prime due cifre del risultato
      • PASSO 3 – Il quadrato del numero sottratto corrisponde alle ultime due cifre del risultato
        • Es. 1 (96)2  ⇒  100-96 = 4 ⇒ 96-4 = 92 ⇒ 42 = 16 ⇒ 9216

#

    1. Il numero è maggiore di 100 (TRUCCO 32)
      • PASSO 1 – Stabilire la distanza del numero 100
      • PASSO 2 – Sommare il numero ottenuto al numero di cui dobbiamo calcolare il quadrato, otteniamo così le prime tre cifre del risultato
      • PASSO 3 – Il quadrato del numero sommato corrisponde alle ultime due cifre del risultato
        • Es. 1 (106)2  ⇒  106-100 = 6 ⇒ 106+6 = 112 ⇒ 62 = 36 ⇒ 11236

#

5) CALCOLO DI RADICI QUADRATE

Calcolo di radici quadrate che hanno come soluzione un numero inferiore a 100 non decimale. (TRUCCO 33)

PASSO 1 – Si utilizza la tabella dei quadrati dei numeri inferiori a 10

12  =  1
22 =   4
32 =   9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81

Si considera la cifra delle unità del numero di cui dobbiamo trovare la radice. Questa cifra sarà uguale alla cifra delle unità dei quadrati in tabella. Se è la cifra è 5 non c’è possibilità di errore. Se invece questa è un’altra qualsiasi, allora abbiamo sempre due possibilità.

ES. √625 – Nella tabella troviamo il numero 25 che ha la cifra delle unità uguale a quella del numero di cui vogliamo trovare la radice. In questo caso la radice avrà la cifra delle unità uguale a 5 senza possibilità di errore

ES. √324 – Nella tabella troviamo sia 4 che 64 che hanno la cifra delle unità uguale a quella del numero di cui vogliamo trovare la radice. Dovremo scegliere fra 2 e 8 che sono le rispettive radici dei numeri che hanno la cifra delle unità uguale a quella del numero di cui dobbiamo trovare la radice.

 PASSO 2 – Consideriamo ora la cifra delle centinaia oppure le prime due cifre se il numero è composto da 4 cifre. Sempre guardando la tabella Dobbiamo prendere in considerazione, un numero inferiore rispetto alla cifra delle centinaia fra i quadrati possibili. La radice di questo numero sarà la prima cifra della soluzione.

Es. √324 – La cifra delle centinaia è 3, quindi prenderemo in considerazione il numero 1, dato che i quadrati possibili da 4 passano 1 e 3 è inferiore a 4. La radice di 1 è ovviamente 1 quindi sarà il primo numero della soluzione.

PASSO 3 – Quando la cifra delle unità è diversa da 5 (come ad esempio in 324) rimane da stabilire quale numero dobbiamo prendere in considerazione. (nel caso del 324 è 2 o 8)

PASSO 3.1 – Moltiplichiamo il numero trovato come prima cifra della soluzione per il numero immediatamente successivo

PASSO 3.2 – Se il numero ottenuto è maggiore del numero della prima cifra della soluzione  allora il numero delle unità sarà il più grande dei due, viceversa il numero delle unità sarà il più piccolo.

Es. √324 – Come abbiamo trovato, il numero della prima cifra è 1. Moltiplichiamo quindi per il successivo 1x2 = 2. Notiamo che 1 > 2. Quindi il numero della seconda cifra sarà 8.

SOLUZIONE

Es. √324 – La cifra delle unità è 4. Guardando la tabella abbiamo due possibilità per 4 come ultima cifra:  2, che è la radice di 4, oppure 8 che è la radice quadrata di 64. La cifra delle centinaia è 3 che è inferiore a 4. L’unica possibilità inferiore a 4, come possiamo vedere nella tabella dei quadrati è 1. La prima cifra del numero della soluzione è quindi 1. Rimane da stabilire l’ultima cifra. Moltiplichiamo quindi 1 per il suo successivo, ossia 2 (2×1) otteniamo 2. Essendo 2 > 1, il numero che dobbiamo scegliere fra 4 o 8 è 8 poichè è il più grande.

RISULTATO; 18

ALTRI ESEMPI

Es. √3364

SOLUZIONE

La cifra delle unità è 4. Guardando la tabella abbiamo due possibilità per 6 come ultima cifra:  2, che è la radice di 4, oppure 8 che è la radice quadrata di 64. In questo caso consideriamo le prime due cifre, abbiamo il numero 33. L’unica possibilità inferiore a 33, come possiamo vedere nella tabella dei quadrati è 5. La prima cifra del numero della soluzione è quindi 5. Rimane da stabilire l’ultima cifra. Moltiplichiamo quindi 5 per il suo successivo, ossia 6 (5×6), otteniamo 30. Essendo 33 > 30, il numero che dobbiamo scegliere fra 4 o 8 è 8 poichè è il più grande.

RISULTATO: 58

Es. √9216

SOLUZIONE

La cifra delle unità è 6. Guardando la tabella abbiamo due possibilità per 6 come ultima cifra:  4, che è la radice di 16, oppure 6 che è la radice quadrata di 32. Anche in questo caso consideriamo le prime due cifre, abbiamo il numero 92. L’unica possibilità inferiore a 92, come possiamo vedere nella tabella dei quadrati è 81 la cui radice quadrata è 9. La prima cifra del numero della soluzione è quindi 9. Rimane da stabilire l’ultima cifra. Moltiplichiamo quindi 9 per il suo successivo, ossia 10 (9×10), otteniamo 90. Essendo 92 > 90, il numero che dobbiamo scegliere fra 4 o 6 è 6 poichè è il più grande.

RISULTATO: 96

#

Radice quadrata di un numero a 4 cifre (TRUCCO 34)

PASSO 1  – Considerare le prime due cifre determinando il quadrato di un numero che si avvicina di più al numero formato dalle prime due cifre. Il risultato deve essere sempre inferiore al numero formato dalle prime due cifre del numero.

Es √4356 ⇒ 62 = 36, 36 < 43 , 72 = 49, 49 > 43, il primo numero del quadrato è quindi 6

PASSO 2  – Consideriamo le ultime due cifre determinando il quadrato che ha come risultato la seconda cifra uguale all’ultima cifra del numero di cui operiamo la radice quadrata.

l’ultima cifra è 6 quindi possiamo avere 6×6 = 36 oppure 4×4 = 16

PASSO 3 – Per tentativi escludiamo uno dei due numeri moltiplicando le cifre del numero ottenuto fra loro e poi per 2. Sommiamo poi la prima cifra del numero ottenuto al quadrato del numero ottenuto con il passo 1.

  1. 64×64 ⇒ (6×4)x2 = 48

2. 66×66 ⇒ (6×6)x2 = 72

36+4 = 40 (da escludere poichè le prime due cifre danno 43)

36+7 = 43 (il numero coincide con le prime due cifre)

#

6) DIVISIONE (o QUOZIENTE)

#

(TRUCCO 35) DIVISIONE PER 5, 50, 500, ….

  • Moltiplicare il numero per 2 e poi dividerlo per 10, 100, 1000, …

Es 1) 80 : 50 ⇒ 80 x 2 = 160 ⇒ 160:100 = 1,60

Es 2) 440 : 5 ⇒ 440 x 2 = 880 ⇒ 880:10 = 88

#

(TRUCCO 36) DIVISIONE PER 25, 250, ….

  • Moltiplicare il numero per 4 e poi dividerlo per 100, 1000,…

Es 1) 80 : 25 ⇒ 80 x 4 = 320 ⇒ 320:100 = 3,2

Es 2) 440 : 250 ⇒ 440 x 4 = 1760 ⇒ 1760:1000 = 1,76

2

(TRUCCO 37) QUOZIENTE DI NUMERI FATTORIALI 

La differenza fra i numeri seguiti dal simbolo di fattoriale fornisce il numero dei termini da considerare. Gli altri termini sono ovviamente semplificati a 1.

25 – 23 = 2 (numero dei termini del 25 fattoriale da considerare)

RISULTATO

25 ⋅ 24

23-15 = 8 (numero dei termini del 23 fattoriale da considerare)

RISULTATO

#

7) FORMULE INVERSE

#

(TRUCCO 38) FORMULE SENZA SOMME O DIFFERENZE DI GRANDEZZE

Le formule di questo tipo prevedono solo la presenza di divisioni o moltiplicazioni.

SOLUZIONE

PASSO 1 – I valori che si trovano dalla parte opposta del valore che dobbiamo trovare non vanno spostati

PASSO 2 – I valori che si trovano dalla stessa parte del valore che dobbiamo trovare vanno spostati al di là del simbolo =

  • CASO 1 – Se si trovano come denominatore, dall’altra parte dell’uguale saranno invece al numeratore
  • CASO 2 –  Se si trovano al numeratore, dall’altra parte dell’uguale saranno invece al denominatore

Supponiamo di dover trovare il valore B della equazione generale di esempio generale

Secondo il CASO 1: il  valore A rimane nella sua posizione essendo un numeratore dalla parte opposta di B, D e C invece andranno spostati

Secondo il CASO 2: dal CASO 1 sappiamo che D e C vanno spostati e quindi D, essendo un numeratore dall’altra parte dell’uguale, passerà ad essere un denominatore, mentre C essendo un denominatore dall’altra parte dell’uguale passerà ad essere un numeratore.

 

che ovviamente è uguale a

#

(TRUCCO 39) FORMULE CON SOMME O DIFFERENZE DI VALORI

Le formule di questo tipo prevedono sia la presenza di divisioni o moltiplicazioni sia somme e differenza di valori.

SOLUZIONE

PASSO 0 – Se vi sono somme fra valori interi o valori frazionari che possono essere sommati o raccolti bisogna prima effettuare tali operazioni

PASSO 1 – I valori che si trovano dalla parte opposta del valore che dobbiamo trovare non vanno spostati

PASSO 2 – I valori che si trovano dalla stessa parte del valore che dobbiamo trovare vanno spostati al di là del simbolo = ,  allo stesso modo di quanto indicato al Trucco 27 PASSI 1 e 2. Attenzione però che le somme dovranno essere spostate tutte insieme e racchiuse in parentesi come fossero un solo valore.

Supponiamo di dover trovare il valore S della equazione generale di esempio generale, applicando il PASSO 1 e 2 avremo

PASSO 3  – Come in una normale equazione spostiamo il valore H dall’altra parte del simbolo = semplicemente cambiandogli il segno e quindi avremo

che ovviamente è uguale a

8) RISOLUZIONE DI EQUAZIONI 

VELOCIZZAZIONE DEI CALCOLI

#

  1. FORMULE DIRETTE (TRUCCO 40)

EQUAZIONI DI PRIMO GRADO (ax + c= 0)

Due termini simili dalla stessa parte di un equazione vanno sommati algebricamente, mentre due termini simili da parti opposte di un equazione vanno sottratti.

ES 1  4x-2=8x+8

PASSO 1 

4x – 8x = – 4x

-2-8 = -10

PASSO 2

4x = 10

ES 1  -4x2-2=8x+8

SOLUZIONE EQUAZIONE DI PRIMO GRADO

ax + c= 0

x = – c / a

SOLUZIONE EQUAZIONE DI SECONDO GRADO

TIPO 1   ax2 + bx + c = 0

TIPO 2   ax2 + bx = 0

x1 = 0

x2 =  – b / a2

TIPO 3   ax2 + c = 0

x1,2 = ± √c/a

Es. 1 3x2 – 5 = 0

x1,2 = ± √5/3

#

2. SCORCIATOIE PER EQUAZIONI DI SECONDO GRADO PARTICOLARI (TRUCCO 41)

Se la somma dei coefficienti di posto pari è uguale a quella di posto dispari il polinomio si annulla per −1.

ax2 +bx + c = 0

se si verificano le condizioni sarà quindi:

x1 = -1

x2 = – (c/a)

Es.1 8x2 – 65x -73 = 0

SOLUZIONE

  1. VERIFICA DELLE CONDIZIONI

In posto pari troviamo – 65, mentre in posto dispari troviamo 8 e -73

8-73 =  – 65

Risulta che le condizioni sono verificate

2 APPLICAZIONE DELLE FORMULE SEMPLIFICATE

x1 = -1

x2 = – (c/a)  ⇒ x2 = – (-73/8) = 73/8

3. SCORCIATOIE PER EQUAZIONI DI SECONDO GRADO PARTICOLARI (TRUCCO 42)

ax2 + bx + c = 0

Se b2-1 = 4ac allora Δ = 1

PASSO 0 – Se b = 1, allora questa scorciatoia non può essere applicata

PASSO 1 – Calcolare il quadrato del coefficiente di b e sottrarre 1

PASSO 2 – Calcolare il valore di 4ac.

Se la condizione sarà verificata la formula classica sarà ridotta e le soluzioni saranno:

x1,2 = (-b ± 1) / 2a

 

9) EQUAZIONI ED ESPRESSIONI

#

UTILIZZAZIONE DI SIMBOLI PER L’INDIVIDUAZIONE DI TERMINI SIMILI (TRUCCO 43)

Quando si risolvono espressioni o equazioni algebriche è utile servirsi di simboli che possono facilitare il raggruppamento di addendi in termini simili. Qui di seguito vengono consigliati i simboli più funzionali allo scopo:

□ Δ ○ ∞ oppure #@*$

ESEMPIO

In questo modo diventa semplice individuare i termini simili e raggrupparli per effettuare i calcoli

#

10) PERCENTUALI E FRAZIONI

CALCOLO DI PERCENTUALI (TRUCCO 44)

PASSO 1  – Determinare l’ordine di grandezza

CASO 1 – Il numero della percentuale ha un ordine di grandezza maggiore del numero di cui vogliamo calcolare la percentuale
L’ordine di grandezza è dato dal numero di cifre del numero di cui dobbiamo calcolare la percentuale.

PASSO 2 – Moltiplicare il numero percentuale per il numero di cui vogliamo calcolare la percentuale

PASSO 3 – Il numero di cifre del risultato ottenuto dovrà essere dello stesso numero dell’ordine di grandezza. Pertanto se nella moltiplicazione si ottiene un numero con cifre in più bisognerà escluderle ponendo la virgola.

Es. 1) 32% di 420

(PASSO 1) Determinazione dell’ordine di grandezza

⇒ 3 cifre poichè 420 è composto da 3 cifre

(PASSO 2) Moltiplicazione (si effettua anche applicando il Trucco n. 15)

32 x 420 = 3x4_(3+4)x2_ 4 ⇒  12 14 4  ⇒ 13440

(PASSO 3) Correzione per l’ordine di grandezza trovato

Il risultato deve avere 3 cifre senza tener conto dei decimali, quindi

13440 ⇒  134,40

CASO 2 – Il numero della percentuale ha un ordine di grandezza minore del numero di cui vogliamo calcolare la percentuale

PASSO 1  – Determinare l’ordine di grandezza

L’ordine di grandezza è dato dal numero di cifre del numero della percentuale.

PASSO 2 e PASSO 3 (come nel CASO 1)

Es. 1) 45% di 8

(PASSO 1) Determinazione dell’ordine di grandezza

⇒ 1 cifra poiché 8 è composto da 1 cifra

(PASSO 2) Moltiplicazione (si effettua anche applicando il Trucco n. 15

45 x 8 = (40 x 8) + (5×8) =  320+40 = 360

(PASSO 3) Correzione per l’ordine di grandezza trovato

Il risultato deve avere 1 cifra senza tener conto dei decimali, quindi

360 ⇒  3,6

CASO 3 – Il numero della percentuale ha un ordine di grandezza uguale del numero di cui vogliamo calcolare la percentuale

Il numero avrà lo stesso ordine di grandezza dei due numeri.

Es. 1)

99% di 99

praticamente abbiamo 992 che risolviamo applicando il Trucco 24

100-99 = 1  ⇒ 99 – 1 = 98  ⇒ 12 = 1 ⇒ 9801

L’ordine di grandezza è 2 pertanto si avrà

9801 ⇒ 98,01

CONFRONTO DI FRAZIONI (TRUCCO 45)

Confrontando due frazioni è possibile stabilire quale frazione è maggiore dell’altra

PASSO 1

Moltiplicare il numeratore della prima frazione con il denominatore della seconda e riportare il risultato ottenuto in alto a sinistra della prima frazione.

PASSO 2

Moltiplicare il numeratore della seconda frazione con il denominatore della prima  frazione e riportare il risultato ottenuto in alto a destra della seconda frazione.

PASSO 3

Confrontare i numeri ottenuto ed apporre il segno >, < oppure =

ESEMPIO

 

#

SCORPORO DELL’IVA (TRUCCO 46) 

Se A è l’importo totale della fattura. La formula da applicare è:

#

11. FISICA-MATEMATICA

    • CONVERSIONE CELSIUS (°C) ⇔ FAHRENHEIT (°F) (TRUCCO 47)

Il valore in °C di una temperatura espressa in °F è pari ai 5/9 della differenza con 32  di detta temperatura espressa in °F

 

Una variazione di 5 °C corrisponde a 9°F.

Es x(°C) = 42 °F – 32 = 10  ⇒ 10 · 5/9 = 50/9 = 5,55…

47°C = 14,55 …

sapendo che 32°F = 0°C e che una variazione di 5°C corrisponde a 9°F, posso facilmente passare da una misura all’altra con una semplice somma rispetto al valore di riferimento.

Es. se la T passa da 0°C a 5°C è aumentata di 5°C ovvero da 32°F a 41°F.

  • CONVERSIONE CELSIUS (°C) ⇔ KELVIN (°K) (TRUCCO 48)

sapendo che  0° C = 273,15 °K e 100 °C = 373 °K, basterà sommare i °C a 273,15 per ottenere i °K, viceversa per ottenere i °C bisognerà sottrarre 273,15

a(°C )+ 273,15 = b(°K )

viceversa

a(°C ) = b(°K ) – 273,15

fra 30°C e 39°C basterà sommare le cifre del numero dei gradi per ottenere la cifra delle unità del numero dei °C, la cifra dopo la virgola è ovviamente ,15

30 (3+0 = 3) ⇒ 303,15
31 (3+1 = 4) ⇒ 304,15

…

39 (9+3 = 12) ⇒ 312,15

fra 40°C e 46°C la somma delle cifre del numero dei gradi va scomposta in 1 e u per ottenere la cifra delle unità del numero dei °C, la cifra dopo la virgola è ovviamente ,15

40 (4+0 = 4) che si dovrà scomporre in 1 e 3 ⇒ 313,15
41 (4+1 = 5) ⇒ che si dovrà scomporre in 1 e 4 ⇒ 314,15

…

fra 47°C e 56°C la somma delle cifre del numero dei gradi va scomposta in 2 e u per ottenere la cifra delle unità del numero dei °C, la cifra dopo la virgola è ovviamente ,15

47 (4+7 = 11) che si dovrà scomporre in 2 (somma di 1+1) e 0 ⇒ 320,15
48 (4+8 = 12) che si dovrà scomporre in 2 e 10 ⇒ 321,15
49 (4+9 = 13) che si dovrà scomporre in 2 e 2 (la somma deve dare 4)  ⇒ 322,15

fra 57°C  e 66 °C la somma delle cifre del numero dei gradi va scomposta in 3 e u per ottenere la cifra delle unità del numero dei °C, mentre la cifra dopo la virgola è sempre, 15 e così via

#

12. GEOMETRIA

INDIVIDUAZIONE DELLE COORDINATE DI UNA RETTA (TRUCCO 49)

Dato che per due punti passa una ed una sola retta, basterà porre nell’equazione prima x=0 e poi x=1, avremo così rapidamente le due coordinate dei punti e potremo facilmente disegnare la retta. Non è necessario infatti determinare altri punti.

ESEMPI

ESEMPIO 1

y = x + 1/2

SOLUZIONE

per x= 0, y=1/2

per x = 1, y = 3/2

coordinate dei due punti su cui far passare la retta, o meglio appartenenti alla retta avente come equazione y = x + 1/2:

A (0, 1/2), B (1, 3/2)

ESEMPIO 2

y = 2/3x + 1/2x + 6

SOLUZIONE

per x= 0, y=6

per x =1, y = 2/3+ 1/2+6 ⇒ y = 4+3/6 + 6 = 4+1/2 = 16+2/4 = 18/4 = 9/2

coordinate dei due punti su cui far passare la retta, o meglio appartenenti alla retta avente come equazione y = x + 1/2:

A (0,6), B (1, 9/2)

#

13. ALTRI TRUCCHI

GIORNI DELLA SETTIMANA (TRUCCO 50)

Per prima cosa dobbiamo associare un numero ad ogni giorno della settimana in questo modo: LUNEDI’ 1, MARTEDI’ 2, MERCOLEDI’ 3, GIOVEDI’ 4, VENERDI’, 5 SABATO 6, DOMENICA 7

Calcolare il numero del giorno della settimana

Adesso calcoliamo ad esempio che giorno sarà il prossimo sabato se per esempio siamo a giovedì 18:

a SABATO abbiamo associato 6, mentre a GIOVEDI’ abbiamo associato 4.

Ora basterà sottrarre 6-4 = 2 e quindi sommarlo al numero del giorno in cui si è. Quindi 18+2= 20. La risposta alla domanda sarà: il prossimo sabato sarà giovedì 20.

Se c’è un cambio di settimana fra la data in cui si è e quella da venire che vogliamo conoscere le cose si complicano leggermente

se per esempio siamo a martedì 20 ottobre e vogliamo sapere che giorno sarà lunedì prossimo:

da MARTEDI’ (2) a DOMENICA (7)  (prima settimana) ⇒ 7-2 = 5 e quindi (20+5=25) domenica sarà il 25 ottobre

tra DOMENICA (7) a LUNEDI’ (1) ⇒ c’è solo 1 giorno (e quindi 7-1=6 per il cambio di settimana 7-6=1) e quindi (25+1=26)  lunedì sarà il 26 ottobre

Quando c’è un cambio di mese fra la data in cui si è e quella da venire che vogliamo conoscere dobbiamo sapere in che giorno cambierà il mese

Ad esempio se siamo a MARTEDI’ (2) 28 ottobre e vogliamo conoscere che giorno sarà il prossimo sabato dobbiamo sapere che il 30 ottobre cambierà il mese, ossia 2 gg dopo.

Quindi il mese cambierà GIOVEDI’ (4) 30 ottobre, perchè essendo MARTEDI’ (2) ⇒ 2+2 = 4 che appunto corrisponde a GIOVEDI’.

da GIOVEDI’ (2) a SABATO (6)  ⇒ 6-2 = 4 e quindi (0+4=4) sabato sarà il 4 novembre

Quando c’è sia un cambio di settimana che un cambio di mese fra la data in cui si è e quella che vogliamo conoscere: dobbiamo operare come segue:

  1. Prima calcolare il giorno del cambio di mese
  2. Poi considerare il cambio di settimana

Ci troviamo ad esempio a GIOVEDI’ 28 ottobre e dobbiamo calcolare che giorno sarà sabato della prossima settimana.

Sappiamo che il 30 ottobre cambierà il mese, quindi 30-28=2

GIOVEDI’ ha 4 quindi 4+2= 6 che corrisponde a SABATO (6) , quindi il 30 ottobre sarà sabato

Il cambio di settimana ci sarà DOMENICA (7) quindi 7-6=1, quindi il 1 novembre sarà DOMENICA.

LUNEDI’ (1) sarà il 2 novembre, poichè 1+1 = 2

mentre SABATO (6) sarà il 7 novembre, poichè 6-1 = 5 e 5+2 = 7

 

 

*** SEZIONE IN COSTRUZIONE ***

RELATED ARTICLESMORE FROM AUTHOR

LEAVE A REPLY

Please enter your comment!
Please enter your name here